합동과 대칭 - 초등학교 5학년 2학기 수학(3단원)

초등학교 5학년 2학기 수학 수학(3단원) - 합동과 대칭 

---

3단원 합동과 대칭도 아이 혼자서 스스로 공부를 진행하고, 저에게 특정 부분(명확하게 이해가 안되는 부분)을 질문하는 형태로 진행했습니다.

 

수학을 공부하다 보면, 문제는 풀 수 있는데 왜 그렇게 되는지가 완벽하게 이해가 안되는 경우가 종종 있습니다. 아이에게 조금이라도 궁금한 부분이 있으면 꼭 물어보는 습관을 가질 수 있게 지도하고 있고, 저도 한번씩 원리를 설명해 달라고 하면서 아이의 이해도를 체크하고 있습니다.

---

3단원. 합동과 대칭

 

기본

• 도형의 합동을 알아볼까요
• 합동인 도형의 성질을 알아볼까요
• 선대칭도형과 그 성질을 알아볼까요
• 점대칭도형과 그 성질을 알아볼까요

응용

• 접은 부분을 이용하여 전체 넓이 구하기
• 대칭인 도형에서 넓이 구하기
• 점대칭도형인 수 구하기
• 선대칭도형인 코트의 넓이 구하기

---

도형의 합동을 알아볼까요

 

합동 : 모양과 크기가 같아서 포개었을 때 완전히 곂치는 두 도형

 

합동인 두 도형의 성질을 알아볼까요

 

합동인 도형의 경우,

대응점 : 겹치는 점

대응변 : 겹치는 변

대응각 : 겹치는 각

이라는 것은 정확하게 알고 넘어갑니다.

 

선대칭도형과 그 성질을 알아볼까요

 

선대칭도형 : 한 직선을 따라 접어서 완전히 겹치는 도형

선대칭도형에서의 대칭축을 따라 포개었을 때, 겹치는 점, 변, 각을 각각 대응점, 대응변, 대응각이라고 합니다.

 

점대칭도형과 그 성질을 알아볼까요

 

점대칭도형 : 한 도형을 어떤 점(대칭의 중심)을 중심으로 180˚ 돌렸을 때, 처음 도형과 완전히 겹치는 도형

(선대칭도형의 대칭축은 여러 개일 수 있지만, 점대칭도형에서 대칭의 중심은 1개뿐입니다)

 

문제풀이에 있어서, 대응변의 길이와 대응각의 크기는 같다는 것을 숙지하고, 답을 작성할 때 "점", "변", "각"을 빼먹어서 틀리는 경우가 없도록 조심합니다.

 

반응형

 

기본기 다지기

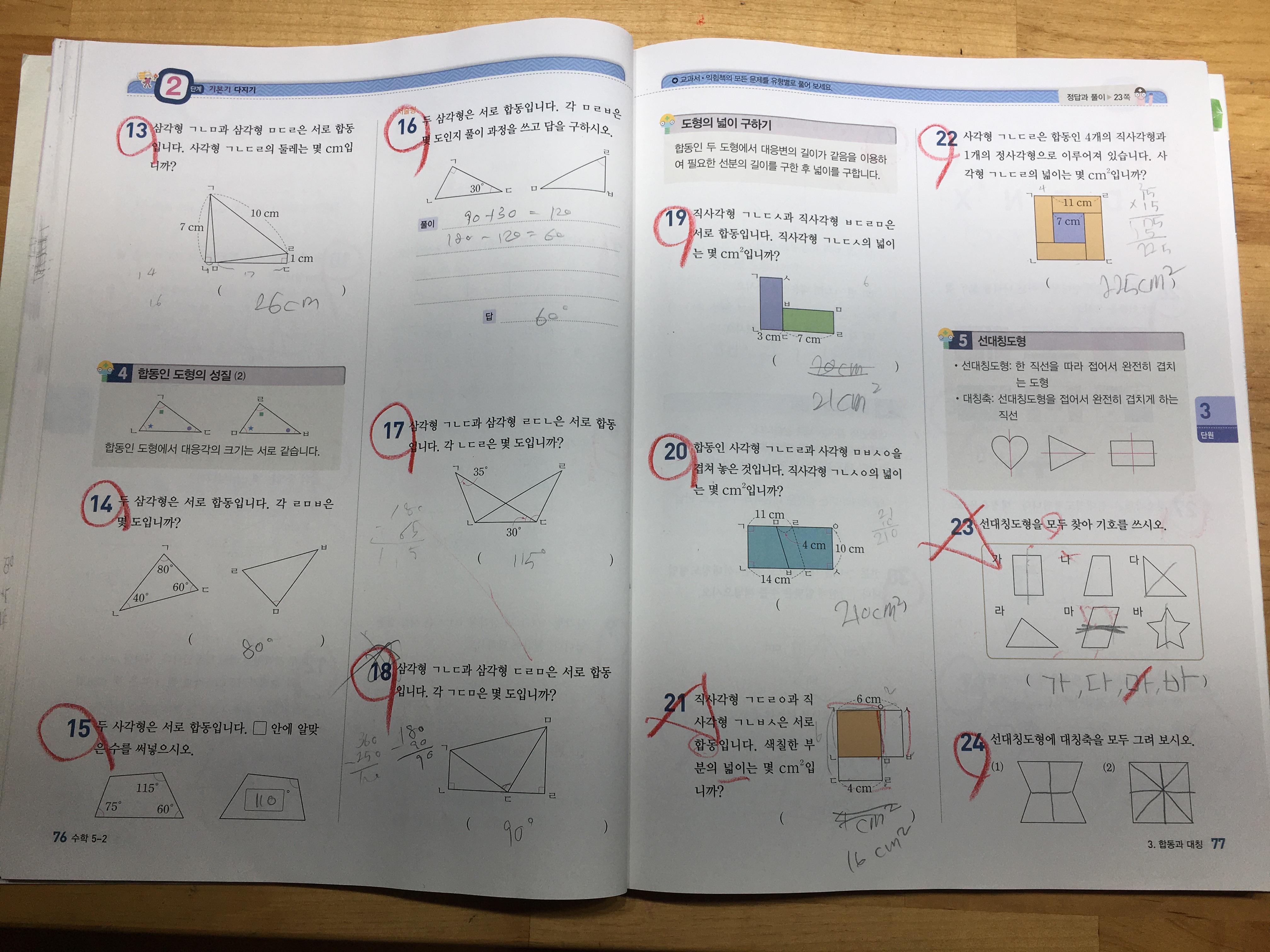
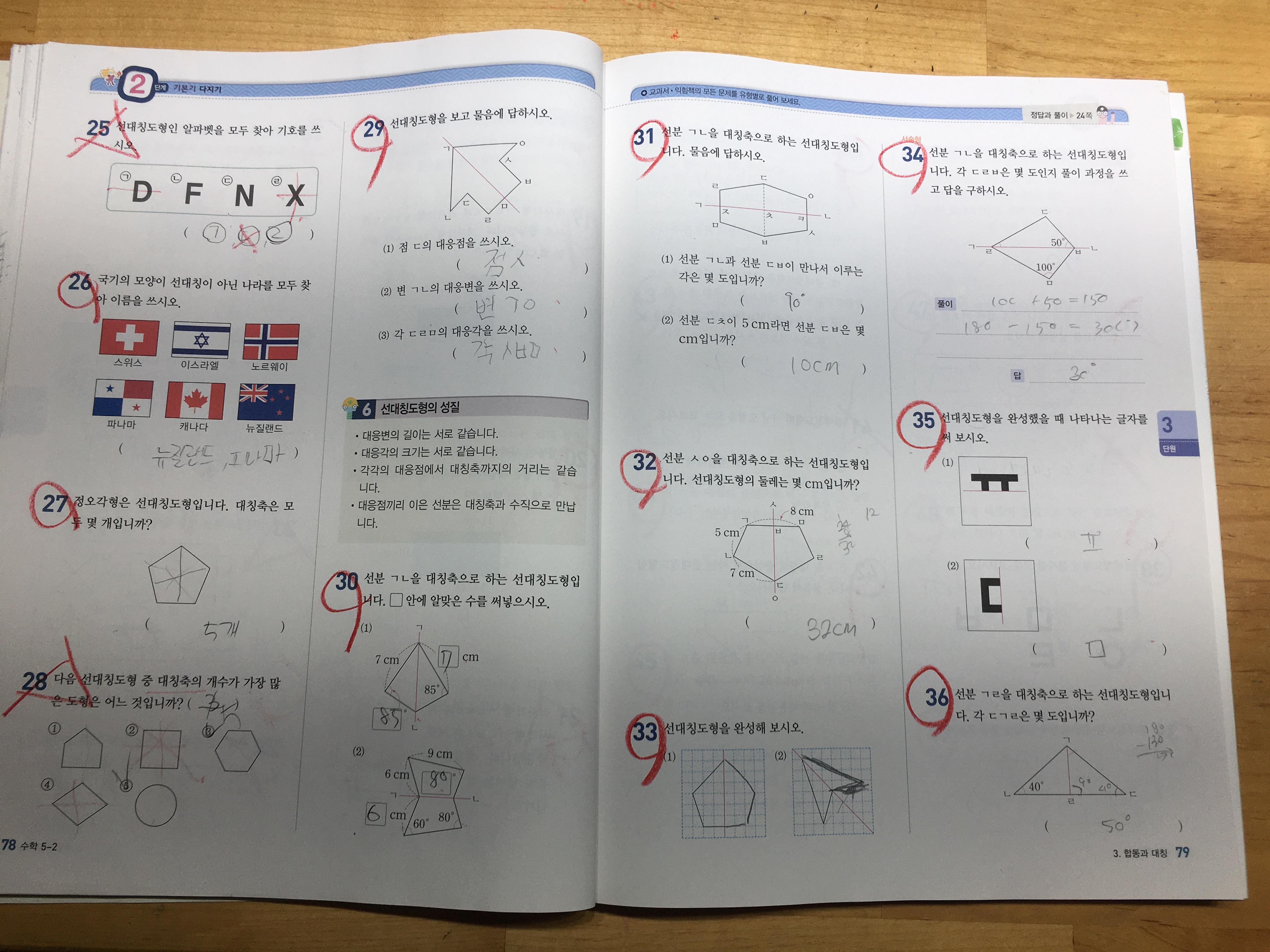
기본문제를 풀이하면서, 합동, 선대칭도형, 점대칭도형의 정의를 정확하게 이해하고, 풀어볼 수 있도록 합니다.

 

합동과 대칭 단원은 분수의 늪에 빠진 아이들에게, 소수로 넘어가기 전에 잠깐 쉬어가는 단원이라고 볼 수 있어요. 다만, 용어의 정의를 숙지하고 충분히 문제를 풀어보는 것이 중요합니다.

 

눈에 익지 않은 도형의 경우에 꼭 하나씩 빼먹는 경우가 생길 수 있기 때문입니다.(운동장 모양, 국기 등)